Engineering Mathematics
Friday, April 4, 2014
Wednesday, July 24, 2013
Monday, February 11, 2013
Polylogarithm
Definition of Polylogarithm
Proof
(1)
(2)
summing (1) and (2)
(3)
(4)
(5)
using the definition of polylogarithm , the function equation is:
Tuesday, January 1, 2013
Saturday, December 1, 2012
Generating Function
GF.ID.1: Chebyshev polynomial
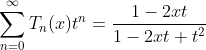 Given:
Given:
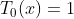
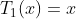
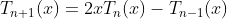
Expanding of Chebyshev polynomial as following:
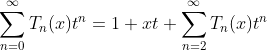
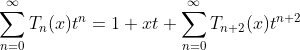
rewriting (1.c) as :
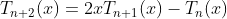
from (2.b) and (3)
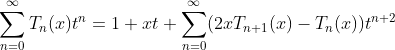
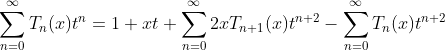

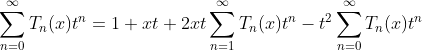
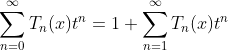
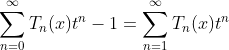
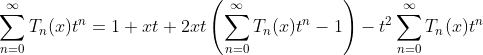
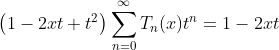
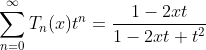
(1.a)
(1.b)
(1.c)
Expanding of Chebyshev polynomial as following:
(2.a)
(2.b)
rewriting (1.c) as :
(3)
from (2.b) and (3)
(4.a)
(4.b)
(4.c)
(4.d)
similar to (3) , Expanding of Chebyshev polynomial as following:
(5.a)
(5.b)
From (4.d) and (5.b) ,
(6.a)
(6.b)
rearranging (6.b)
Subscribe to:
Posts (Atom)