Engineering Mathematics: Central Binomial Coeffecient

Monday, August 8, 2011

Central Binomial Coeffecient

$A_{n}= \binom{2n}{n}$

(1)

CBD.ID.1: Recurrence Relation

$A_{n+1}= \binom{2n+2}{n+1}= \frac{(2n+2)!}{(n+1)!(n+1)!}=\frac{2(2n+1)}{n+1}\frac{2n!}{n!n!}$

(2)

$A_{n+1}= \frac{2(2n+1)}{n+1}\binom{2n}{n} = \frac{2(2n+1)}{n+1} A_{n}$

(3)

$(n+1)A_{n+1}= 2(2n+1) A_{n}$

(4)

where

$A_{0}= \binom{0}{0}=1$

(5)

CBD.ID.2: Generating Function

$A(x)= \sum _{n=0}^{\infty }A_{n}x^{n}=A_{0}+\sum _{n=0}^{\infty }A_{n+1}x^{n+1}$

(6)

Differentiating both sides with respect to x

$A'(x)= \sum _{n=0}^{\infty }(n+1)A_{n+1}x^{n}$

(7)

$xA'(x)= \sum _{n=0}^{\infty }(n+1)A_{n+1}x^{n+1}$

(8)

$xA'(x)= \sum _{n=0}^{\infty }nA_{n}x^{n}$

using the recurrence relation (4)

(9)

$A'(x)= \sum _{n=0}^{\infty }2(2n+1)A_{n}x^{n}$

(10)

$A'(x)= 2\left [2 \sum _{n=0}^{\infty }nA_{n}x^{n} +\sum _{n=0}^{\infty }A_{n}x^{n} \right ]$

$A'(x)= 2\left [2 xA'(x) +A(x) \right ]= 4xA'(x)+ 2A(x)$

(11)

$(1-4x)A'(x)= 2A(x)$

(12)

$\frac{A'(x)}{A(x)}= \frac{2}{1-4x}$

(13)

integrating both sides with respect to x ,

$\ln A(x)= \ln\frac{1}{\sqrt{1-4x}} + \ln C$

(14)

$A(x)= \frac{C}{\sqrt{1-4x}}$

(15)

since

$A(0)= A_{0}=1 , C=1$

therefore,

$\sum _{n=0}^{\infty }\binom{2n}{n}x^{n}= \frac{1}{\sqrt{1-4x}}$

(16)

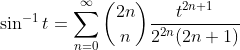
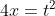
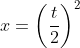
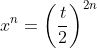
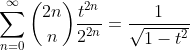
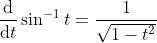
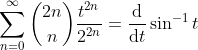
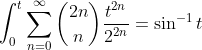
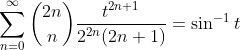
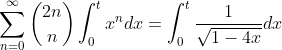
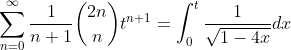
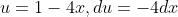
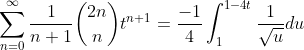
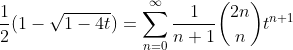
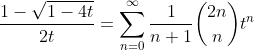
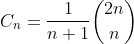
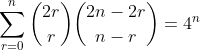
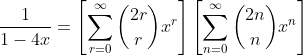
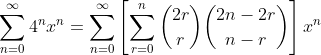
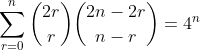
CBD.ID.3: Trigonometric Identity

$\sin ^{-1} t =\sum _{n=0}^{\infty }\binom{2n}{n}\frac{t^{2n+1}}{2^{2n} (2n+1)}$

proof

replacement in (16) by :

$4x=t^{2}$

$x=\left ( \frac{t}{2} \right )^{2}$

$x^{n}=\left ( \frac{t}{2} \right )^{2n}$

therefore

$\sum _{n=0}^{\infty }\binom{2n}{n}\frac{t^{2n}}{2^{2n}}=\frac{1}{\sqrt{1-t^{2}}}$

(17)

$\frac{\mathrm{d} }{\mathrm{d} t}\sin ^{-1} t = \frac{1}{\sqrt{1-t^{2}}}$

(18)

from (17) and (18) , therefore,

$\sum _{n=0}^{\infty }\binom{2n}{n}\frac{t^{2n}}{2^{2n}}=\frac{\mathrm{d} }{\mathrm{d} t}\sin ^{-1} t$

(19)

integrate (19) from 0 to t

$\int _{0}^{t}\sum _{n=0}^{\infty }\binom{2n}{n}\frac{t^{2n}}{2^{2n}}=\sin ^{-1} t$

(20)

therefore,

$\sum _{n=0}^{\infty }\binom{2n}{n}\frac{t^{2n+1}}{2^{2n} (2n+1)}=\sin ^{-1} t$

(21)

CBD.ID.4: Catalan Number Identity

$\frac{1-\sqrt{1-4t}}{2t}=\sum _{n=0}^{\infty }C_{n}t^{n}$

Proof

integrating (16) from 0 to t

$\sum _{n=0}^{\infty }\binom{2n}{n}\int _{0}^{t}x^{n} dx = \int _{0}^{t}\frac{1}{\sqrt{1-4x}} dx$

(22)

$\sum _{n=0}^{\infty }\frac{1}{n+1}\binom{2n}{n}t^{n+1} = \int _{0}^{t}\frac{1}{\sqrt{1-4x}} dx$

replacing 1-4x by u in (23)

(23)

$u= 1-4x , du= -4 dx$

$\sum _{n=0}^{\infty }\frac{1}{n+1}\binom{2n}{n}t^{n+1} = \frac{-1}{4}\int _{1}^{1-4t}\frac{1}{\sqrt{u}} du$

(24)

$\frac{1}{2}(1-\sqrt{1-4t})=\sum _{n=0}^{\infty }\frac{1}{n+1}\binom{2n}{n}t^{n+1}$

(25)

divide both sides by t

$\frac{1-\sqrt{1-4t}}{2t}=\sum _{n=0}^{\infty }\frac{1}{n+1}\binom{2n}{n}t^{n}$

(26)

$C_{n}= \frac{1}{n+1}\binom{2n}{n}$

(27)

$\frac{1-\sqrt{1-4t}}{2t}=\sum _{n=0}^{\infty }C_{n}t^{n}$

(28)

CBD.ID.5: Square Identity of Central Binomial Coefficient

$\sum _{r=0}^{n }\binom{2r}{r}\binom{2n-2r}{n-r} =4^{n}$

Proof

squaring both sides of (16)

$\frac{1}{1-4x}= \left [ \sum _{r=0}^{\infty }\binom{2r}{r}x^{r} \right ]\left [ \sum _{n=0}^{\infty }\binom{2n}{n}x^{n} \right ]$

(29)

applying geometric series (1) identity on the left side , and Cauchy product method (2) on the right side;

$\sum _{n=0}^{\infty}4^{n}x^{n}= \sum _{n=0}^{\infty}\left [ \sum _{r=0}^{n }\binom{2r}{r}\binom{2n-2r}{n-r} \right ]x^{n}$

(30)

equating the coefficients of 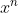$x^{n}$ from both sides , we get

$\sum _{r=0}^{n }\binom{2r}{r}\binom{2n-2r}{n-r} =4^{n}$

(31)

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)