firstly , I recommend you to read these Gamma function to have fundamental understanding of the Gamma function.
G.ID.1: Differentiation (integral representation)
differentiate gamma function in term of x variable
if x=1
G.ID.2: integral representation
proof
given that
variable substitution
(1)
(2)
from (1), lower and upper integrals boundaries change
(3)
(4)
(5)
G.ID.3: integral representation
proof
given that
variable substitution
G.ID.4: Weierstrass Identity
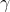 = Euler–Mascheroni constant
= Euler–Mascheroni constant
Given
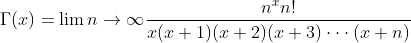
Proof
(1)
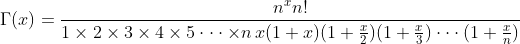
(2)
(3)
the 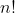 cancels out, and based on (3) , therefore,
cancels out, and based on (3) , therefore,
(4)
(5)
multiply 4 by 5 , therefore
(6)
(7)
(8)
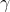 = Euler–Mascheroni constant
= Euler–Mascheroni constant
therefore;
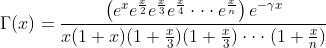
(9)
G.ID.5: Reflection Formula
Given
(1)
(2)
Proof
multiplication of (1) and (2)
multiplication of (1) and (2)
(3)
sine identity
(4)
Recurrence identity of gamma function
(5)
based on (3) and (4) , (5)
(5)
(6)
replace x and (1-x) with the following identities
(7)
therefore
(8)
(9)
substituting (9) into (8) results in
G.ID.6: Recurrence Identity
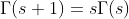
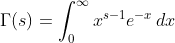 proof
proof
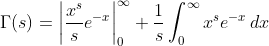
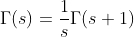
given
if s=s+1/2
integrating by parts results:
after n times of integration by parts:
similarly for s+1/3 and s+1/4
G.ID.7:
proof
(1)
(2)
(3)
(4)
(5)
(6)
No comments:
Post a Comment