Engineering Mathematics: Zeta-Gamma Function

GZ.ID.1: Fundamental Zeta-Gamma function
the relation between Zeta function and Gamma function can be represented in the following form:

$\zeta (s)\Gamma (s)=\int _{0}^{\infty }\frac{t^{s-1}}{e^{t}-1}dt$

$(1-\frac{1}{2^{s-1}})\zeta (s)\Gamma (s) = \int _{0}^{\infty }\frac{t^{s-1}}{e^{t}+1}\, dt$

Proof

Given

$\Gamma (s)=\int _{0}^{\infty }t^{s-1} e^{-t}dt$

(1)

$\zeta (s)=\sum _{n=1}^{\infty }\frac{1}{n^{s}}$

(2)

$\frac{\Gamma (s)}{n^{s}}= \int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{n^{s}} dt$

(3)

$t=nx , dt=n\, dx$

(4)

substituting (4) into (3)

$\frac{\Gamma (s)}{n^{s}}= \int _{0}^{\infty }\frac{(nx)^{s-1}e^{-nx}}{n^{s}} n\, dx$

(5)

$\frac{\Gamma (s)}{n^{s}}= \int _{0}^{\infty }\frac{n^{s}x^{s-1}e^{-nx}}{n^{s}} \, dx$

(6)

$\sum _{n=1}^{\infty}\frac{\Gamma (s)}{n^{s}}= \sum _{n=1}^{\infty}\int _{0}^{\infty }x^{s-1}e^{-nx} \, dx$

(7)

$\Gamma (s)\zeta (s)= \int _{0}^{\infty }x^{s-1}\sum _{n=1}^{\infty}e^{-nx} \, dx$

(8)

Based on Geometric Series of Exponential (GS.ID.2),

$\Gamma (s)\zeta (s)= \int _{0}^{\infty }x^{s-1}\frac{e^{-x}}{1-e^{-x}} \, dx$

(9)

$\Gamma (s)\zeta (s)= \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}-1} \, dx$

(10)

$\frac{2}{e^{2x}-1}=\frac{1}{e^{x}-1}-\frac{1}{e^{x}+1}$

$\frac{1}{e^{x}-1}=\frac{2}{e^{2x}-1}+\frac{1}{e^{x}+1}$

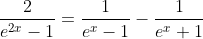
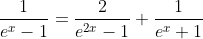
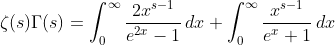
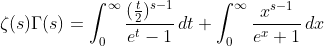
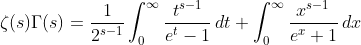
(11)

based on (10) and (11) ,

$\zeta (s)\Gamma (s)=\int _{0}^{\infty }\frac{2x^{s-1}}{e^{2x}-1}\, dx + \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

(12)

$\zeta (s)\Gamma (s)=\int _{0}^{\infty }\frac{(\frac{t}{2})^{s-1}}{e^{t}-1}\, dt + \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

(13)

$\zeta (s)\Gamma (s)=\frac{1}{2^{s-1}}\int _{0}^{\infty }\frac{t^{s-1}}{e^{t}-1}\, dt + \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

(14)

$\zeta (s)\Gamma (s)=\frac{1}{2^{s-1}}\zeta (s)\Gamma (s) + \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

(15)

$(1-\frac{1}{2^{s-1}})\zeta (s)\Gamma (s) = \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

(16)

GZ.ID.2: Zeta-Gamma function (Trigonometric)

$\zeta (s)\Gamma (s)=2^{s-1}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\sinh (t)}\, dt$

$\zeta (s)\Gamma (s)=\frac{2^{s-1}}{1-2^{s-1}}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\cosh (t)}\, dt$

Proof

Given

$\zeta (s)\Gamma (s)=\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{1-e^{-t}}\, dt$

(1)

$\sinh (t)=\frac{e^{t}-e^{-t}}{2}=\frac{e^{2t}-1}{2e^{t}}$

(2)

$\cosh (t)=\frac{e^{t}+e^{-t}}{2}=\frac{e^{2t}+1}{2e^{t}}$

(3)

$t=2t , dt= 2\, dt$

(4)

substituting (4) into (1) ,

$\zeta (s)\Gamma (s)=2\int _{0}^{\infty }\frac{(2t)^{s-1}e^{-2t}}{1-e^{-2t}} \, dt$

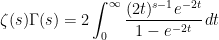
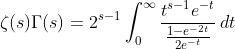
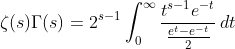
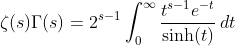
(5)

$\zeta (s)\Gamma (s)=2^{s-1}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\frac{1-e^{-2t}}{2e^{-t}}} \, dt$

(6)

$\zeta (s)\Gamma (s)=2^{s-1}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\frac{e^{t}-e^{-t}}{2}} \, dt$

(7)

substituting (2) into (7) :

$\zeta (s)\Gamma (s)=2^{s-1}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\sinh (t)} \, dt$

(8)

from (16), at (GZ.ID.1) ,

$(1-\frac{1}{2^{s-1}})\zeta (s)\Gamma (s) = \int _{0}^{\infty }\frac{x^{s-1}}{e^{x}+1}\, dx$

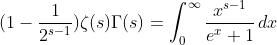
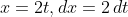
(9)

$x=2t, dx=2\, dt$

(10)

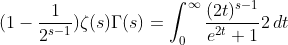
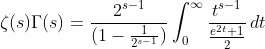
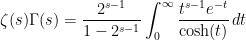
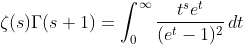
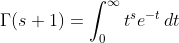
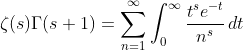
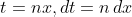
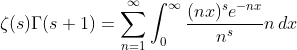
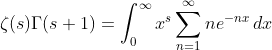
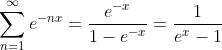
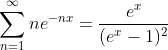
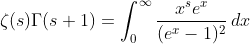
based on (9) and (10) , then

$(1-\frac{1}{2^{s-1}})\zeta (s)\Gamma (s)=\int _{0}^{\infty} \frac{(2t)^{s-1}}{e^{2t}+1} 2\, dt$

$\zeta (s)\Gamma (s)=\frac{2^{s-1}}{(1-\frac{1}{2^{s-1}})}\int _{0}^{\infty} \frac{t^{s-1}}{\frac{e^{2t}+1}{2}} \, dt$

multiplying and dividing the denominator by 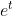$e^t$ , and based on (3) therefore

$\zeta (s)\Gamma (s)=\frac{2^{s-1}}{1-2^{s-1}}\int _{0}^{\infty }\frac{t^{s-1}e^{-t}}{\cosh (t)}\, dt$

GZ.ID.3: Zeta-Gamma function

$\zeta (s)\Gamma (s+1)=\int _{0}^{\infty }\frac{t^{s}e^{t}}{(e^{t}-1)^{2}}\, dt$

Given

$\Gamma (s+1)=\int _{0}^{\infty }t^{s}e^{-t}\, dt$

(1)

$\zeta (s)\Gamma (s+1)=\sum _{n=1}^{\infty }\int _{0}^{\infty }\frac{t^{s}e^{-t}}{n^{s}}\, dt$

(2)

$t=nx , dt=n\, dx$

(3)

substitute (3) into (2) ,

$\zeta (s)\Gamma (s+1)=\sum _{n=1}^{\infty }\int _{0}^{\infty }\frac{(nx)^{s}e^{-nx}}{n^{s}}n\, dx$

(4)

$\zeta (s)\Gamma (s+1)=\int _{0}^{\infty }x^{s}\sum _{n=1}^{\infty }ne^{-nx}\, dx$

(5)

$\sum _{n=1}^{\infty }e^{-nx}=\frac{e^{-x}}{1-e^{-x}}=\frac{1}{e^{x}-1}$

(6)

differentiate (6) ,

$\sum _{n=1}^{\infty }ne^{-nx}=\frac{e^{x}}{(e^{x}-1)^{2}}$

(7)

substitute (7) into (5) ,

$\zeta (s)\Gamma (s+1)=\int _{0}^{\infty }\frac{x^{s}e^{x}}{(e^{x}-1)^{2}}\, dx$

(8)

Engineering Mathematics

Wednesday, May 18, 2011

Zeta-Gamma Function

No comments:

Post a Comment